马尔科夫模型
关于马尔科夫,可以认为是一个自动机,以一定的概率P在各个状态s之间转移,马尔科夫模型由状态、转移概率矩阵{s,p}两部分组成。
关于隐马尔科夫模型(HMM),比马尔科夫多了一个观测集合 O。可以认为是一个双重随机过程,状态之间的转移是随机的, 在某状态时的输出也是随机的。隐马尔科夫链由初始状态概率向量π、状态转移概率矩阵p、观测概率矩阵B三部分组成,{π,p,B}。马尔科夫和隐马尔科夫都具有无后效性,也就是系统的下一个状态之和当前的状态有关,和更早以前的无关。
马尔科夫决策过程(Markov Decision Process, MDP),比HMM多了一个动作集合,也具有无后效性。但是相比于隐马尔科夫,MDP的下一状态s’不仅和当前状态s相关,还和当前状态下所采取的动作a相关。
马尔科夫决策过程,MDP
一个马尔科夫决策过程由一个元组构成: M = { S, A, Psa, R,γ}
- S, 状态集合, s ∈ S, si 表示 第 i 步的状态
- A, 动作集合, a ∈ A, ai 表示 第 i 步的动作
- Psa, 状态转移概率, Psa表示在状态 s 下,采取动作 a 之后的所转移到的状态的概率分布情况。
- R,回报函数,reward, 假设在 {s,a}的情况下转移到 s’,则定义其回报函数为 r(s’|s,a)。回报是根据状态和动作得到的,如果 s,a确定之后的 s’是唯一的,回报函数可以记作 r(s,a)。
- γ, 衰减因子, 0-1之间。
策略(policy),π
策略:π: S->A, ,指在t时刻,给定状态下,所能采取的动作的概率分布: 记作 π(a|s) = P(At=a | St=s),可以认为是状态到动作的映射,这也正是一个智能体(agent)所要学习的东西,策略完全决定了一个智能体(agent)的行为,MDP 的策略取决于当前状态。
给定一个MDP, M= { S, A, Psa, R,γ},以及策略 π,则状态序列S1,S2,… 就是一个马尔科负过程{S, Pπ}。状态和回报序列 S1,R1,S2,R2,… 就是一个马尔科夫回报过程 {S,Pπ, Rπ, γ},而且有:

值函数,value function
强化学习的过程,就是学习环境状态到动作的映射,可以发现,这就是在学习一个能够获得最大回报的策略π。不过强化学习的回报是具有延迟性的,立即回报函数 r(s,a) 并不能完全确定策略的好坏,我们还必须评估未来的回报函数。
如果定义衰减回报和如下式所示,其中Ri是第i-1步的立即回报:
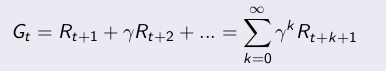
其中γ是衰减因子,决定了长期回报的重要性,γ为0时忽略长期回报,为1时,所有时刻的回报同等重要。
定义一个状态值函数 Vπ(s),来表示在状态s 下,策略 π的长期影响产生的回报:
状态值函数(state value function)如下:

再定义一个动作值函数(action value fucntion),表示在状态 s 下, 采取动作 a 之后依照 策略 π所产生的期望回报:

需要注意的是,在状态值函数里,只有初始状态s和策略π是给定的,初始动作是由s和π决定的,而在动作值函数里面,初始状态s和初始动作a,策略π都是给定的。
其实上面两个值函数的定义方程也就是贝尔曼方程(Bellman exception equation)。
根据状态s下,采取动作a之后的状态转移概率,可以发现 状态值函数和动作值函数之间的关系如下所示:


将关系式带入原贝尔曼方程,可以得到贝尔曼方程变种,算是展开了的贝尔曼方程。。


优化值函数
优化值函数,就是寻找在任意初始条件下,能够最大化值函数的策略π*,
通过最大化状态值函数或者最大化动作值函数都可以:

关于贝尔曼优化方程(Bellman optimal equation):


贝尔曼优化方程是非线性的,通过多次迭代求解贝尔曼优化方程可以求解MDP的最优策略。