模型无关的策略估计(model free prediction),可以看作是求解环境知识不完整的模型在特定策略π下的每一个状态值函数,模型无关(model free),是指对于模型的环境知识知道的不完整,比如不知道转移概率或者立即回报函数。有两种方法求解,蒙特卡洛法和时间差分法,这两种方法的适用情况略有不同:
蒙特卡洛法(Mento Carlo methods, MC) 适用条件:
- 直接从eposides of experience中学习。即从经验中学习经验,经验就是训练样本,在初始状态 s下,遵循策略π最终获得总回报G,这就是一个样本。
- model free。不需要知道状态转移概率或者立即回报函数。
- 只适用于eposides task。eposides task是指eposides必须有终点,能够在有限时间内达到终止状态,比方说围棋,经过若干回合之后一定会分出输赢或平局。训练所用的eposides必须是完整的eposides。
- 认为经验均值是期望值。
可以发现,MC方法对于连续性的任务是不能用的,比方说自动驾驶,根据当前环境路况等来调整行驶方向和速度,要保证行驶,这样的问题,我们是得不到一个完整的有终点的样本。于是,有人就想出了 时间差分学习法来解决连续性任务。
时间差分法(Temporal different Learning, TD leaning) 适用条件:
- 直接从eposodes中学习。
- model free。不需要完整的环境知识。不需要知道状态转移概率或者立即回报函数。
- 除了 eposides task, 还可以用于连续性任务。
1. 蒙特卡洛法(Mento Carlo methods, MC)
策略估计,就是要学习策略对应的状态值函数Vπ(S)。MC分为first visit和every visit,first visit是只记录一个eposide里面状态 s 的第一次访问,every visit则记录每一次访问。下面讲一下 first visit MC 。 Gt是当前状态的长期总回报值:
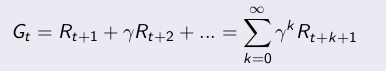
估计状态 s 的值函数:
- 对于每一个eposide里面,状态 s 的第一次访问:
- 增加访问计数:N(s) <—— N(s) + 1
- 增加总回报: S(s) <—— S(s) + Gt
- 估计 V(s), V(s) = S(s)/N(s)
- 当N(s)——>∞,V(s)——> Vπ(s)
every visit的差别只需要把第一访问改成每一次访问即可
Incremental Monte Carlo Update:
一个序列 x1,x2,x3…..的均值 u1,u2, u3,…计算方式有如下简化:
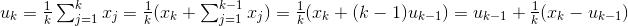
从这个式子考虑发现,其实 MC methods的更新也有类似的变种:
估计状态 s 的值函数:
- 每一个状态 St 的,其长期总回报函数为Gt,访问到St时:
- 增加访问计数:N(St) <—— N(St) + 1
- 更新状态值函数:

- 当N(s)——>∞,V(s)——> Vπ(s)
状态更新的式子也可以用这个式子:  ,α 是学习率。
,α 是学习率。
2. 时间差分法(Temporal different Learning, TD leaning)
TD:
时间差分法的状态值更新方式和incremental MC的的第二种更新方式很像,也是引进了学习率 α,但还引进了衰减因子 γ,将 Gt 替换成了Rt+1 + γV(St+1)。
估计状态 s 的值函数:
- 每一个状态 St 的,其长期总回报函数为Gt,每次访问到St时:
- 增加访问计数:N(St) <—— N(St) + 1
- 更新状态值函数:

- 当N(s)——>∞,V(s)——> Vπ(s)
在这个状态值更新式里:
 是TD target
是TD target
 是TD error
是TD error
n-step TD:
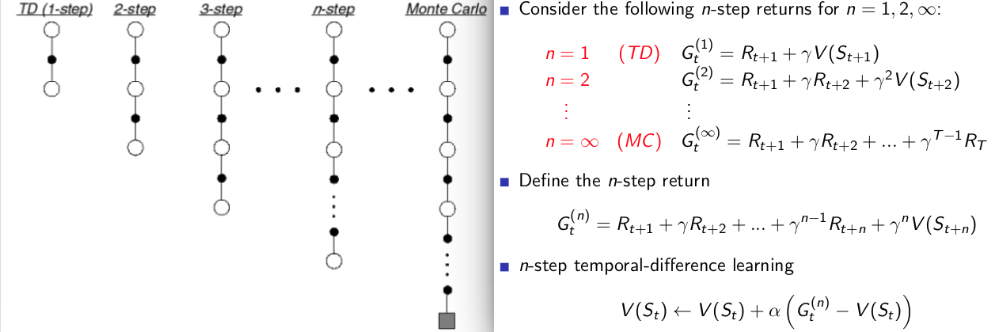
n-step TD对未来预测采取 n 步,总回报 G也是计算的n步的回报值。从上面的式子和图可以发现:
- n=1时,总回报值就是 TD 算法计算的总回报值。
- n=∞时,总回报值就是 MC 算法计算的总回报值,这时候的n-step TD其实就是 MC算法。
TD(λ):
如果考虑到给 每个 step 的回报加上权重值然后相加来作为总回报值,如下图所示:
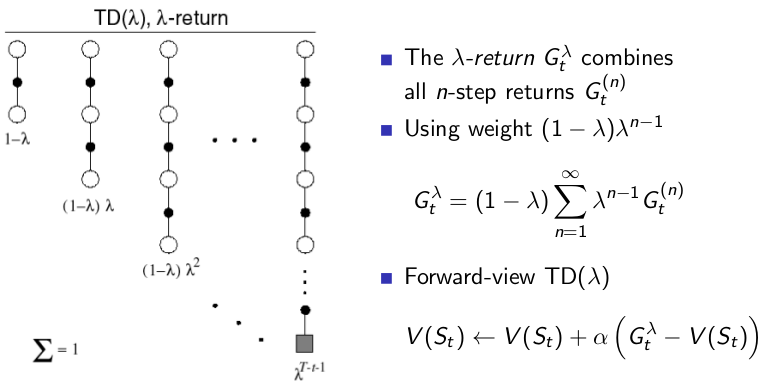
这样子的总回报值是结合了所有step的回报,利用 λ来评估每个step的回报所占的比重。
从上图左边的链图里可以发现,有两个特殊情况:
- λ=0时,可以发现 TD(0) = TD。λ=0时,除了step=1的时候的回报比重是 1 ,其他step的回报的比重是0,所以这个时候实际上总回报只有 step=1的时候的总回报,和 TD算法的总回报值是一样的。
- λ=1时,TD(1) = MC。λ=1的时候,可以发现总回报值只有最后一条链step=∞时候的回报,其他的占比都是0,这和MC是一样的。