Welcome to CJW's Blog!

• 强化学习课程系列之四：模型无关的策略估计

  2016-10-17

  强化学习

   模型无关的策略估计(model free prediction)，可以看作是求解环境知识不完整的模型在特定策略π下的每一个状态值函数,模型无关(model free)，是指对于模型的环境知识知道的不完整，比如不知道转移概率或者立即回报函数。有两种方法求解，蒙特卡洛法和时间差分法，这两种方法的适用情况略有不同：

  蒙特卡洛法(Mento Carlo methods, MC) 适用条件:

  1. 直接从eposides of experience中学习。即从经验中学习经验，经验就是训练样本，在初始状态 s下，遵循策略π最终获得总回报G，这就是一个样本。
  2. model free。不需要知道状态转移概率或者立即回报函数。
  3. 只适用于eposides task。eposides task是指eposides必须有终点，能够在有限时间内达到终止状态,比方说围棋，经过若干回合之后一定会分出输赢或平局。训练所用的eposides必须是完整的eposides。
  4. 认为经验均值是期望值。

   可以发现，MC方法对于连续性的任务是不能用的，比方说自动驾驶，根据当前环境路况等来调整行驶方向和速度，要保证行驶，这样的问题，我们是得不到一个完整的有终点的样本。于是，有人就想出了 时间差分学习法来解决连续性任务。

  时间差分法(Temporal different Learning, TD leaning) 适用条件:

  1. 直接从eposodes中学习。
  2. model free。不需要完整的环境知识。不需要知道状态转移概率或者立即回报函数。
  3. 除了 eposides task， 还可以用于连续性任务。

  1. 蒙特卡洛法(Mento Carlo methods, MC)

   策略估计，就是要学习策略对应的状态值函数Vπ(S)。MC分为first visit和every visit，first visit是只记录一个eposide里面状态 s 的第一次访问，every visit则记录每一次访问。下面讲一下 first visit MC 。 Gt是当前状态的长期总回报值：

  
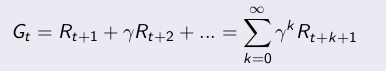
  估计状态 s 的值函数:

  1. 对于每一个eposide里面，状态 s 的第一次访问:
     • 增加访问计数：N(s) <—— N(s) + 1
     • 增加总回报： S(s) <—— S(s) + Gt
  2. 估计 V(s)， V(s) = S(s)/N(s)
  3. 当N(s)——>∞,V(s)——> Vπ(s)

  every visit的差别只需要把第一访问改成每一次访问即可

  Incremental Monte Carlo Update:
  一个序列 x1,x2,x3…..的均值 u1，u2, u3,…计算方式有如下简化：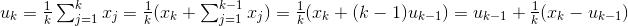

  

  从这个式子考虑发现，其实 MC methods的更新也有类似的变种:
  估计状态 s 的值函数:

  1. 每一个状态 St 的,其长期总回报函数为Gt,访问到St时：
     • 增加访问计数：N(St) <—— N(St) + 1
     • 更新状态值函数：
  2. 当N(s)——>∞,V(s)——> Vπ(s)

  状态更新的式子也可以用这个式子： ,α 是学习率。

  2. 时间差分法(Temporal different Learning, TD leaning)

  TD:
   时间差分法的状态值更新方式和incremental MC的的第二种更新方式很像，也是引进了学习率 α,但还引进了衰减因子 γ，将 Gt 替换成了Rt+1 + γV(St+1)。

  估计状态 s 的值函数:

  1. 每一个状态 St 的,其长期总回报函数为Gt,每次访问到St时：
     • 增加访问计数：N(St) <—— N(St) + 1
     • 更新状态值函数：
  2. 当N(s)——>∞,V(s)——> Vπ(s)

  在这个状态值更新式里：
  是TD target
  是TD error

  n-step TD:

  

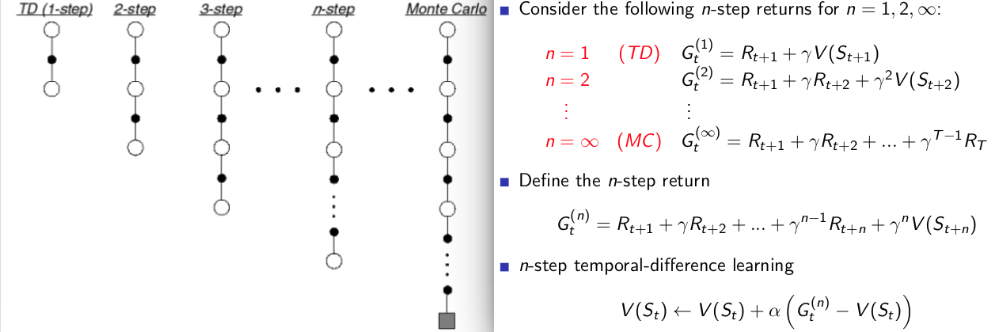
   n-step TD对未来预测采取 n 步，总回报 G也是计算的n步的回报值。从上面的式子和图可以发现：

  1. n=1时，总回报值就是 TD 算法计算的总回报值。
  2. n=∞时，总回报值就是 MC 算法计算的总回报值，这时候的n-step TD其实就是 MC算法。

  TD(λ):
  如果考虑到给 每个 step 的回报加上权重值然后相加来作为总回报值，如下图所示：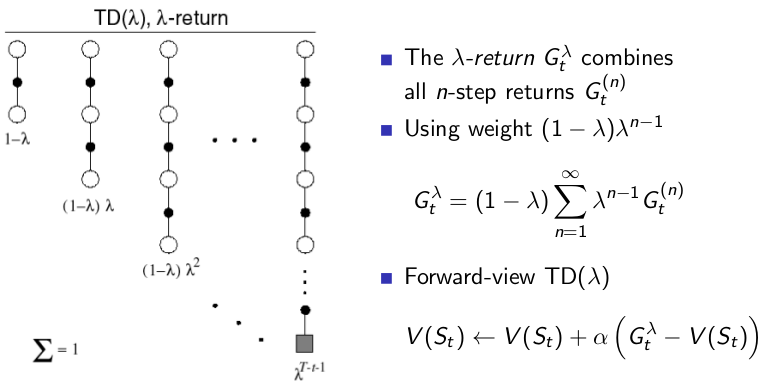

  

  这样子的总回报值是结合了所有step的回报，利用 λ来评估每个step的回报所占的比重。
  从上图左边的链图里可以发现，有两个特殊情况：

  1. λ=0时，可以发现 TD(0) = TD。λ=0时，除了step=1的时候的回报比重是 1 ，其他step的回报的比重是0，所以这个时候实际上总回报只有 step=1的时候的总回报，和 TD算法的总回报值是一样的。
  2. λ=1时，TD(1) = MC。λ=1的时候，可以发现总回报值只有最后一条链step=∞时候的回报，其他的占比都是0,这和MC是一样的。
  Read All

  ---

• 强化学习课程系列之三：MDP动态规划求解

  2016-10-17

  强化学习

  强化学习，目的就是求解MDP(马尔科负决策过程)，而MDP的求解有三种情况:

  1. 动态规划求解法：求解一个已知环境完整知识的MDP。有两种方法：
     • 策略迭代
     • 值迭代
  2. Model free prediction：对于一个环境知识不完整的MDP， 估计状态值函数。有两种方法：
     • 蒙特卡罗法： MC
     • 时间差分学习法： TD
  3. Model free control： 对于一个环境知识不完整的MDP， 优化状态值函数。

  第三节，本篇博客就是讲的动态规划求解法，还有两种接下来的两节博客会讲到。

  1. 贝尔曼方程，Bellman Equation

  这里回顾一下上一节讲MDP时讲到的 Bellman equation

  贝尔曼期望方程： Bellman Exception Equation

  上一节提到了对于给定策略，如何计算状态值函数Vπ和动作值函数qπ，方程式如下：

  

  

  这就是bellman exception equation， 从式子可以看出来，当前状态的值函数Vπ和下一状态的值函数相关。

  贝尔曼优化方程：Bellman Optimal Equation

   关于寻找最优策略，是指时所有状态值函数最大的策略,而关于最优策略下的优化状态值函数和优化动作值函数，是满足bellman optimal equation方程的，也就是如下式两个方程：

  
  

  有了贝尔曼期望方程和贝尔曼优化方程，我们就可以利用动态规划求解法求解MDP的最优策略了，求解方法有策略迭代和值迭代两种。

  2. 策略迭代： Policy Iteration

  在讲策略迭代之前，先讲以下这个方法用到的两个基本步骤：策略估计和策略改进。

  2.1 策略估计：Policy evaluation

   策略估计：给定一个策略π，计算该策略下的所有状态值函数Vπ(S)，可以通过迭代贝尔曼期望方程求解。
  贝尔曼方程告诉了我们对于确定的策略，如何求状态值函数，但是一般某个策略下，某个状态π(S)对应的动作a可能有很多种，一般采用多次迭代的方法更新状态值函数：

  V1——>V2——>…——>Vπ

  1. 首先初始化所有状态值函数V(s)为0
  2. 进行迭代，也就是重复步骤 3直至收敛。对于每一次迭代 k+1，进行步骤 3 :
  3. 遍历状态，对每一个状态 s in S，都进行以下操作:
     • 采用下面式子对状态 s 的状态值函数进行更新。
       
  4. 最后收敛至 Vπ,就是该策略的状态值函数。

  最后，举个栗子，关于策略估计，假设一个4*4格子，左上角和右下角是终止状态点，非终止状态14个，明日歌状态可以采取的动作是移到相邻的格子(碰壁则留在原状态)，上下左右移动概率相等，都是0.25，转到终止态回报为0，其他任意转移的reward都是 -1，γ是1。

  

  在k=0，初始状态是随机策略，V(s)全部随机为0.
  k=1, 第一行第二列， v = 0.25*(-1+0)+ 0.25*(-1+0)+ 0.25*(-1+0)+ 0.25*(-1+0)= -1.0 ；
  k=2, 第一行第二列， v = 0.25*(-1+0)+ 0.25*(-1-1)+ 0.25*(-1-1)+ 0.25*(-1-1)= -1.75 = -1.7；
  k=2，第一行第三列， v = 0.25*(-1-1)+ 0.25*(-1-1)+ 0.25*(-1-1)+ 0.25*(-1-1)= -2.0；

  2.2 策略改进：Policy improvement

   策略改进：是为了寻找一个更好的策略，对于一个策略，我们到底能不能找到更好的策略呢。如果对于策略π,对某个状态，采用的动作a0得到状态值函数，如果我们采取其他动作，会不会更好。怎么判断动作的好坏，我们就可以通过计算动作值函数来判断了，通过选取动作值函数最大的动作来改进策略获得新策略：
  对于一个确定的策略，对每个状态，遍历这个状态的所有可能动作，采用贪心算法来获得新的优化的策略，步骤如下：

  1. 遍历状态 s， 对每个状态 s in S，采用下面式子进行更新。
     

  2.3 策略迭代

   策略迭代的过程，其实就是策略估计和策略改进的组合，比如先随机给定一个策略，利用策略估计计算它的状态值函数，然后利用策略改进获得新策略，然后重复计算策略估计和策略改进，直至收敛。

  1. 随机初始化一个策略
  2. 重复步骤 3，4，直至收敛
  3. 策略估计：
     多次迭代，对每个状态值函数进行更新直至收敛得到该策略的状态值函数。
  4. 策略改进：
     对每个状态进行改进，找动作值函数最大的动作来改进策略获得新策略。
  5. 最后策略收敛稳定时，返回的值函数和策略就是想要的结果。 整个过程图解如下：
     

  看图，策略迭代的过程就是根据策略迭代计算这个策略下每个状态的值函数，然后根据状态值函数来，利用贪心算法改进策略，不断的重复这两个步骤，最后收敛，所得到的就是优化策略。

  3. 值迭代

   可以发现，其实策略迭代的方法计算量很大，在策略估计的过程中，每一个状态都要扫描很多次，这样代价太大。但是值迭代，每次迭代时，每个状态只需要扫描一次。

  V1——>V2——>…——>V*

  1. 首先初始化所有状态值函数V(s)为0
  2. 迭代操作，即重复步骤 3直至收敛。对于每一次迭代 k+1 :
  3. 对每一个状态 s in S，都进行以下操作:
     • 采用下面式子对状态 s 的状态值函数进行更新。
       
  4. 最后收敛的输出策略就是所求最优策略 π*。

  一般来说，迭代次数很多才会收敛，实际计算的时候，可以根据精度需求来设置收敛阈值。
  举个栗子，计算最短路径， 只有终止态回报为0， 其他都是-1，γ=1，如下图所示：

  

  第一次迭代，初始化最大V值都是 V = 0；
  第二次迭代，第一行第二列，下一状态不管往哪走，最大V值都是 V=-1 + 1*(0) = -1;
  第三次迭代，第一行第二列， 向左走到终止态时，当前状态V最大， V = -1 + 1*(0) = -1；
  第三次迭代，第一行第三列， 不管往哪走当前状态V一样， V = -1 + 1*(-1) = -2；
  第四次迭代，第一行第三列， 往左走，当前状态V最大， V = -1 + 1*(-1) = -2；
  第四次迭代，第二行第二列， 往上或者左走，当前状态V最大， V = -1 + 1*(-1) = -2；

  4. 总结

  通过策略迭代和值迭代都可以求出最优策略。下面有个表格总结以下完整环境知识下的MDP各种问题的求解：

  

  Read All

  ---

• 强化学习课程系列之二：马尔科夫决策过程，MDP

  2016-10-14

  强化学习

  马尔科夫模型

   关于马尔科夫，可以认为是一个自动机，以一定的概率P在各个状态s之间转移，马尔科夫模型由状态、转移概率矩阵{s,p}两部分组成。
   关于隐马尔科夫模型(HMM),比马尔科夫多了一个观测集合 O。可以认为是一个双重随机过程，状态之间的转移是随机的， 在某状态时的输出也是随机的。隐马尔科夫链由初始状态概率向量π、状态转移概率矩阵p、观测概率矩阵B三部分组成，{π,p,B}。马尔科夫和隐马尔科夫都具有无后效性，也就是系统的下一个状态之和当前的状态有关，和更早以前的无关。
   马尔科夫决策过程(Markov Decision Process, MDP)，比HMM多了一个动作集合，也具有无后效性。但是相比于隐马尔科夫，MDP的下一状态s’不仅和当前状态s相关，还和当前状态下所采取的动作a相关。

  马尔科夫决策过程，MDP

   一个马尔科夫决策过程由一个元组构成： M = { S, A, Psa, R，γ}

  1. S, 状态集合， s ∈ S, si 表示 第 i 步的状态
  2. A, 动作集合， a ∈ A, ai 表示 第 i 步的动作
  3. Psa, 状态转移概率， Psa表示在状态 s 下，采取动作 a 之后的所转移到的状态的概率分布情况。
  4. R，回报函数，reward， 假设在 {s,a}的情况下转移到 s’,则定义其回报函数为 r(s’|s,a)。回报是根据状态和动作得到的,如果 s，a确定之后的 s’是唯一的，回报函数可以记作 r(s,a)。
  5. γ, 衰减因子， 0-1之间。

  策略(policy),π

   策略：π： S->A, ，指在t时刻，给定状态下，所能采取的动作的概率分布： 记作 π(a|s) = P(At=a | St=s),可以认为是状态到动作的映射，这也正是一个智能体(agent)所要学习的东西，策略完全决定了一个智能体(agent)的行为，MDP 的策略取决于当前状态。
   给定一个MDP， M= { S, A, Psa, R，γ}，以及策略 π，则状态序列S1，S2，… 就是一个马尔科负过程{S, Pπ}。状态和回报序列 S1，R1，S2，R2，… 就是一个马尔科夫回报过程 {S,Pπ, Rπ, γ},而且有：

  

  值函数，value function

   强化学习的过程，就是学习环境状态到动作的映射，可以发现，这就是在学习一个能够获得最大回报的策略π。不过强化学习的回报是具有延迟性的，立即回报函数 r(s,a) 并不能完全确定策略的好坏，我们还必须评估未来的回报函数。

  如果定义衰减回报和如下式所示,其中Ri是第i-1步的立即回报：

  
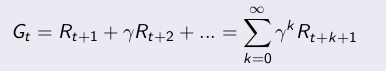
  其中γ是衰减因子，决定了长期回报的重要性，γ为0时忽略长期回报，为1时，所有时刻的回报同等重要。
  定义一个状态值函数 Vπ(s),来表示在状态s 下，策略 π的长期影响产生的回报:
  状态值函数(state value function)如下：
  

  再定义一个动作值函数(action value fucntion)，表示在状态 s 下， 采取动作 a 之后依照 策略 π所产生的期望回报:

  

  需要注意的是，在状态值函数里，只有初始状态s和策略π是给定的，初始动作是由s和π决定的，而在动作值函数里面，初始状态s和初始动作a，策略π都是给定的。

  其实上面两个值函数的定义方程也就是贝尔曼方程(Bellman exception equation)。
  根据状态s下，采取动作a之后的状态转移概率，可以发现 状态值函数和动作值函数之间的关系如下所示：
  

  将关系式带入原贝尔曼方程，可以得到贝尔曼方程变种，算是展开了的贝尔曼方程。。
  
  

  优化值函数

  优化值函数，就是寻找在任意初始条件下，能够最大化值函数的策略π*，
  通过最大化状态值函数或者最大化动作值函数都可以:

  

  关于贝尔曼优化方程(Bellman optimal equation)：

  
  

  贝尔曼优化方程是非线性的，通过多次迭代求解贝尔曼优化方程可以求解MDP的最优策略。

  Read All

  ---

• 强化学习课程系列之一：基本介绍

  2016-10-10

  强化学习

   最近在看reinforcement learning 的视频课程，记录了一些笔记，顺便整理成博客，课程内容复杂有些难理解，博客也许会有些错误的地方，望指正谅解，大家一起学习.

  机器学习分类

  机器学习大概可以分为以下几个类别：

  1. 监督学习：从有标注的训练集中训练学习模型，可以对新数据进行预测。eg. 决策树，回归分析等
  2. 无监督学习：和有监督相比，训练集没有标注，eg 各种聚类算法。
  3. 半监督学习： 介于以上的两者之间。
  4. 强化学习：基于环境而行动，以获得最大化的预期利益。

  强化学习课程官网，主讲人是David Silver。
  课程视频油管上可以找到，不能翻墙的小伙伴可以点这个强化学习百度网盘。

  强化学习

    强化学习： 是指一个智能体(agent)从环境(environment)中学习从状态(state)到动作(action)的映射。是一种无监督学习，没有label，而是反馈信号，而且反馈具有延时性，并不是即时的。比方说下棋，这一步所下的棋所产生的影响并不会完全的即时反馈出来，在未来的步骤中也会有所影响。强化学习组成如下：
  

  1. agent,智能体(上图中的大脑)
  2. environment,环境(上图中的地球)
  3. ：agent的状态(state)，表示agent自己内部的表现，这是强化学习学习时所用到的信息。
  4. ：environment的状态,这是环境自己的状态，一般对agent不可见
  5. At: 动作(action)，表示 agent在某状态 S 采取的动作
  6. Rt; 回报函数(Reward)，在 S 状态， 采取 A 动作所获得的奖励。
  7. Ot: 观测值(observation)。

  整个过程： 在某时刻 t ：

  1. agent行为：
     • 执行动作 At
     • 接收Observation Ot
     • 接受reward Rt
  2. environment：
     • 接收动作 At
     • 发射Observation O(t+1)
     • 发射reward R(t+1)
  3. 进入下一时刻 t+1 ，重复1，2，3步骤。

  对于整个过程下来， 最后就会得到一个observation，action，reward组成的序列 Ht= O1,R1,A1,…At-1，Ot，Rt.
  环境分为两种：

  1. fully observable Environment：这种就是agent能够直接观测到环境的状态，agent state = environment state = observation :
     
      这种情况下，就是一个马尔科夫决策过程(Markov decision process, MDP)。

  2. partial observable Environment：agent不能直接观测到环境的状态，所以agent 和environment的状态不同。

  策略，policy

   policy，是一个智能体的行为，是从 state 到 action 的映射，表示在某状态下采取的动作的概率分布。
   a = π(s)

  值函数, value function

    value function，是对未来reward的预测，用来评估当前状态的好坏。
    

  Read All

  ---

• 深度学习的高维表达的可视化方法

  2016-10-10

  DeepLearning

  1. AM算法： activation maximizing

   AM：节点最大化，通过最大化某个隐藏层节点单元来探究该节点所学习到的 input pattern。简单的做法就是，对于给定某个隐藏层节点，找到一个 input sample 能够最大化的激励这个节点的值。这是一个优化问题，对于一个深度网络，网络参数为 θ。假设 θ 是已经训练好了的网络的参数值，是固定值；x 则表示输入样本，hij(θ,X)表示第 j 层、第 i 个节点单元的激励值，那么hij就是关于 θ 和 x 的函数，θ 已知。那我们就可以通过下面这个公式来计算输入 x，x既是对于该节点所学习到的特征的可视化结果。

  

   该问题是一个非凸优化问题，我们可以通过 gradient ascent 找到局部最优解。类似于知道input x 时优化 θ 的过程。先随机一个 输入 x值，计算 hij 的值，然后求hij对于 x 的倒数，利用gradient ascent算法对x 进行更新直至收敛。一个手写体识别的AM可视化的例子如下：

  

  上图中，第一行的三列分别是用AM对DBN网络的 1st layer、2nd layer、3rdlayer的36个节点单元的可视化结果。
  然后 第二行的三列分别是用AM对SDAE网络的 1st layer、2nd layer、3rdlayer的36个节点单元的可视化结果。

  2. inverting representations

   inverting representations, 这个方法和AM算法有着异曲同工之妙，对于一个已经训练好的参数固定的网络，假设某个隐藏层的表达representation函数为 Φ，则Φ是θ和输入X的函数。给定网络参数θ和待逆推的表达 Φ0=Φ(x0)，来计算一个输入image sample,使这个输入图片 x 所生成的表达和给定的表达 Φ 尽量相似。最小化下面这个公式：

  

  通过最小化这个式子，就可以使输入图片 X 和 原图片 X0 在那个给定的高维表达上尽量的相接近。
  上式中,loss 函数l是比较输入图片生成的表达 Φ(X) 和给定的表达 Φ(X0).loss的计算方式如下：

  

  后面的 R(x) 是正则化项, λ是超参。

  

   关于计算 x 的方式，和AM算法类似，也是优化问题，最小化 loss ，对 x 求导，利用 grident ascent 对 x 进行更新直至收敛。
   code inversion 可以用来重构输入图片，也有论文，为了合成风格迁移的图片，利用code inversion 算法来同时重构目标图片的整体布局和风格图片的纹理信息来合成风格迁移图片。

  3. MFV： Multifacet fearure visualization

   AM 算法和 code inversion 的初始输入input sample 是一个随机值。但是由于满足的条件的输入图片非常的多，可能会生成无法识别的图片。原来的AM算法还有以下的几个问题：

  1. 图片颜色分布不自然
  2. 识别出来的图片片段大量重复
  3. 高维节点单元其实是可以学习多个方面(facet)的信息的，如在面部检测单元可以同时检测到人脸和狮子的脸，但是简单的AM算法是无法同时可视化出这些 facet。

   为了解决多facet的问题，就有论文提出的MFV算法就可以可视化出节点检测到的多个facet的信息。

  该算法利用了AM 算法作为基础，大概步骤如下，首先我们假设该节点检测到的是类别 A，然后我们从数据集中把所有类别A的图片取出来作为新的数据集 U。

  输入： 数据集 U，和 facet 的数目 k

  1. 对U中的每张图片计算指定隐藏层的高维表达 φi，例如指定fc7 layer 。
  2. 利用PCA 将 Φi 从 4096维降到50维。
  3. 用 t-SNE把整个 θ降到二维 2d embedding来进行可视化。
  4. 通过k-means聚类将 2d embendding的所有图片聚类成 k 个类别。
  5. 对于每一个类别，执行下面步骤得到 k 个 facets 的可视化 {X1,X2,…Xk}。
     • 选取离质心最近的m=15张图片来计算得到一张 mean image X0，
     • 初始化输入为 X0， 运行 AM算法。

   因此,可以发现 MVF 可以获得 K 个输入样本，每个样本代表一个facet。如下图：

  

  图a，可以获得节点检测到的电影院室内室外或者白天晚上多个facet的可视化结果。
  图b，可以获得车子的不同颜色和不同角度(车前车后)多个facet的可视化。

   对于AM算法可视化结果有片段重复现象,利用 center-biased regularization可以改善这个现象，具体做法就是先生成一个模糊的中心对象，然后微调目标的中心像素点来生成清新的中心固定的对象，如下图所示：

  

  参考论文：

  1. Understanding Representations Learned in Deep Architectures
  2. Understanding Deep Image Representations by Inverting Them
  3. Multifaceted Feature Visualization: Uncovering the Different Types of Features Learned By Each Neuron in Deep Neural Networks
  Read All

  ---

• spp net, spatial pyramid pooling net，目标检测，语义分割

  2016-08-31

  DeepLearning

  spp net 和 RCNN

   在上一篇博客中，讲到了region CNN 可以用于目标检测和语义分割,但是，RCNN有两个很大的缺点：

  1. 计算量很大。  每张图片都要提取近2k张region proposal，而这zk张proposal其实有大量的重叠，而每个proposal都进行了卷积导致了大量的重复计算。
  2. RCNN的CNN网络只能接受固定大小的size输入(卷积层可以接收任意大小的输入，但是全连接层输入大小必须固定)。   region proposal的大小和长宽比是不一样的，RCNN为了解决这个问题，将所有region proposal 缩放成相同的大小，缩放过程中会导致图片扭曲变形

   net希望加速网络，解决上述两个问题。对于问题一，spp net不再对所有的每张图片提取2k个region proposal进行卷积，而是每一张图片只卷积一次。对于问题二，spp net引入了spatial pyramid pooling layer，使网络可以接受任意大小的图片，输出却是固定的。

  关于 spatial pyramid pooling layer，spp layer

   spp，也叫spatial pyramid matching(SPM),其实是Bag of Words(BoW,词袋)的一种拓展,可以接受任意大小的输入，生成固定大小的输出。相比于BoW，spp可以维护图片的空间信息。这些spatial bins的数目是固定的，但是bins的大小则是正比于输入图片的大小，与之相反的是滑动窗口(slide windows)大小固定，数目则取决于输入图片的大小。
   spp net中，比方说是vgg16的网络，用spp layer替换原来的最后一个池化层pool5。spp layer将卷积之后的features池化(pool)生成固定大小的features，然后将固定大小的features输入给全连接层或者分类器。过程如下图所示：
  
   上图是3个level的bins，{4*4,2*2,1*1}。池化采用的max pooling,最后输出的维度是k*M，M表示bins的数目，k表示最后一个卷积层的filter数目。
   关于spp layer 输入输出的大小计算：
  假设 输入feature map(最后一个卷积层的map)的大小是 a*a, 一个pyramid level的bins数为 n*n，我们可以将这个pooling level 看成是sliding window pooling,而且这个window的size和stride值如下：

  1. window size，窗口大小为 ceil(a/n)
  2. strde, 移动步长为 floor(a/n)。

   对于l个level的pyramid,就实现 l 个这样的 layer，将这 l 个输出拼接之后输入给全连接层。下图实例中就用了三个level，{3*3, 2*2, 1*1}， map size则是 13*13, 计算结果如下:
  

  spp net 用于图片分类

  论文里用Imagenet2012的1000类数据训练spp layer替换最后一个pooling layer的vgg16 网络。

  1. 数据预处理：先resize成256*256 ,然后随机crop 224*224, 水平翻转，改变颜色
  2. spp layer 之后是两个全连接层和 1000-way的softmwx 层，每个全连接层之后都要一个dropout layer
  3. 学习率初始值 0.01。
  4. 多个level pooling训练改善准确率。用了4个level pyramid {6*6,3*3,2*2,1*1}
  5. 多个size训练提升准确率。traing size有224和180.

  spp net + svm 用于目标检测

  1. RCNN网络对每个region proposal都进行卷积通过预训练好的CNN网络提取feature vection。
  2. spp net则用预训练好的CNN网络对每张图片只提取一次 feature map，然后将proposal在图片上的位置映射到feature map上来提取相应的区域的feature map，然后对proposal 的feature map用spatial pyramid pooling 得到固定长度的 feature vector。
      然后固定长度的特征向量输入全连接层， 最后和RCNN一样，每个类别训练一个SVM进行分类，其实懒的话也可以直接在全连接层后面加上softmax layer 分类。接下来的目标定位也和RCNN里面一样。
      这样来看对每张图片，不需要进行2000次卷积，只需要进行2000次映射，spatial pyramid pooling，最后通过全连接层，即可得到固定长度的特征向量。
      预训练好的CNN网络可以直接是ImageNet预训练的网络，也可以进行fine-tuning，将最后的softmax层改成21路的输出，fine tuning时只调整全链接层的参数。

  目标检测也可以用多个size的图片进行训练。把输入图片的尺度增加,把原图resize成短边为s ={480,576,688,864,1200}的大小来分别计算 feature map。这样就有多个不同大小的feature map，但对于每个region proposal，只从这些feature map中选取一个映射之后大小接近于 224*224的进行sp pool。

  Read All

  ---